1352. The number of primes
Vasya loves prime
numbers. He decided to find the sum of the first n
prime
numbers, that are divisible by k. Help him.
Input. One integer k (1 ≤ k
≤ 1000).
Output. Print the minimum possible
value of n.
|
Sample
input |
Sample
output |
|
7 |
5 |
SOLUTION
prime numbers
Algorithm
analysis
Iterate over the first primes (2, 3, 5, 7, ...), and sum them up. As soon as the sum
is divisible by k, print the number of
used terms.
Example
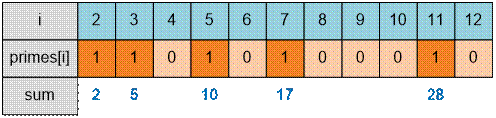
The sum of the first five
primes is 2 + 3 + 5 + 7 + 11 = 28, it is divisible by 7.
Algorithm realization
Function prime returns 1, if n is prime.
int prime(int
n)
{
if (n == 2) return 1;
if (n % 2 ==
0) return 0;
for(int i = 3; i <= sqrt(n); i += 2)
if(n % i ==
0) return 0;
return 1;
}
The main part of the
program. Read
the value of k.
scanf("%d",&k);
In the variable s count the sum of primes, in the variable
c count their amount.
s = c = 0;
Iterate throught
the
integers, starting from
2. If the number is prime, then add it to s. As soon as the
sum s is divisible by k,
stop
iterations.
for(i = 2;; i++)
{
if (prime(i))
{
s += i; c++;
if (s % k
== 0) break;
}
}
Print the smallest number of the first primes, the sum of which is divisible by k.
printf("%d\n",c);
Java realization
import java.util.*;
public class Main
{
public static boolean prime(int n)
{
if (n == 2) return true;
if (n % 2 ==
0) return false;
for(int i = 3; i <= Math.sqrt(n); i += 2)
if(n % i == 0) return false;
return true;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int k = con.nextInt();
int s = 0, c = 0;
for(int i = 2;; i++)
{
if (prime(i))
{
s += i; c++;
if (s % k == 0) break;
}
}
System.out.println(c);
con.close();
}
}
Python realization
import math
def prime(n):
if n == 2: return True
if n % 2 == 0: return False
for i in range(3, int(math.sqrt(n))+1, 2):
if n % i == 0: return False
return True
k = int(input())
s = c = 0
i = 2
while True:
if (prime(i)):
s += i
c += 1
if s % k == 0: break
i += 1
print(c);